JEE 2016 :: Advanced 2016 :: Mathematics 2016

• Advanced 2016 - Physics 2016
• Advanced 2016 - Chemistry 2016
• Advanced 2016 - Mathematics 2016

In a  $\triangle XYZ$ , let x,y,z be the lengths of sides opposite to the angle  X,Y,Z respectively and 2s=x+y+z. If  $\frac{s-x}{4}=\frac{s-y}{3}=\frac{s-z}{2}$ and area of incircle of the $\triangle XYZ$ is  $\frac{8\pi}{3}$ then

Answer:

Explanation:

Given a $\triangle XYZ$  ,where 2x=x+y+z

and   $\frac{s-x}{4}=\frac{s-y}{3}=\frac{s-z}{2}$

$\therefore$                       $\frac{s-x}{4}=\frac{s-y}{3}=\frac{s-z}{2}$ 

=  $\frac{3x-(x+y+z)}{4+3+2}=\frac{s}{9}$

 or  $\frac{s-x}{4}=\frac{s-y}{3}=\frac{s-z}{2}=\frac{s}{9}=\lambda(let)$

$\Rightarrow$    $s=9\lambda,s=4\lambda+x, s=3\lambda+y$ 

 and  $s=2\lambda+z$

$\therefore$    $s=9\lambda,x=5\lambda, y=6\lambda, z=7\lambda$

Now,    $\triangle= \sqrt{s(s-x)(s-y)(s-z)}$   [heron's formula]

$= \sqrt{9\lambda.4\lambda.3\lambda.2\lambda}=6\sqrt{6}\lambda^{2}$          .........(i)

 Also,  $\pi r^{2}=\frac{8\pi}{3}$

 $\Rightarrow$     $ r^{3}=\frac{8}{3}$          .......(ii)

and   $R=\frac{xyz}{4\triangle}$

 $=\frac{(5\lambda)(6\lambda)(7\lambda)}{4.6.\sqrt{6}\lambda^{2}}=\frac{35\lambda}{4\sqrt{6}}$  .......(iii)

Now,   $r^{2}=\frac{8}{3}=\frac{\triangle^{2}}{S^{2}}=\frac{216\lambda^{2}}{81\lambda^{2}}$

 $\Rightarrow$    $\frac{8}{3}=\frac{8}{3}\lambda^{2}$               [from Eq. (ii)]

$\Rightarrow$       $\lambda=1$

 (a)      $\triangle XYZ=6\sqrt{6}\lambda^{2}=6\sqrt{6}$

 $\therefore$      Option (a) is correct.

(b) Radius of circumcircle 

     $(R)=\frac{35}{4\sqrt{6}}\lambda=\frac{35}{4\sqrt{6}}$

$\therefore$  Option (b) is incorrect.

(c) Since,  $r= 4R\sin\frac{X}{2}.\sin\frac{Y}{2}.\sin\frac{Z}{2}$

  $\Rightarrow\frac{2\sqrt{2}}{\sqrt{3}}=4.\frac{35}{4\sqrt{6}}\sin\frac{X}{2}\sin\frac{Y}{2}\sin\frac{Z}{2}$

   $\Rightarrow\frac{4}{35}=\sin\frac{X}{2}\sin\frac{Y}{2}\sin\frac{Z}{2}$

 $\therefore$     Option (c) is correct.

(d)  $\sin^{2}\left(\frac{X+Y}{2}\right)=\cos^{2}\left(\frac{Z}{2}\right)$ .  as

     $\frac{X+Y}{2}=90^{0}-\frac{Z}{2}=\frac{s(s-z)}{xy}=\frac{9\times 2}{5\times 6}=\frac{3}{5}$

$\therefore$   Option (d) is correct

Consider a pyramid OPQRS located in the first octant  $ (x\geq 0, y\geq 0,z\geq0)$ with O as origin, and OP and OR along the X-axis and the Y-axis, respectively. The base OPQR of the pyramid is a square with OP=3. The point S is directly above the mid-point T of diagonal OQ such that TS=3Then

Answer:

Explanation:

Given , square base  OP=OR=3

  $\therefore$    P(3,0,0) , R=(0,3,0)

Also, mid-point of OQ is  $T\left(\frac{3}{2},\frac{3}{2},0\right)$

 Since S is directly above the mid-point T of diagonal OQ and ST =3

i.e,  $S\left(\frac{3}{2},\frac{3}{2},3\right)$

Here , DR's of OQ (3,3,0) and DR's of OS   $(\frac{3}{2},\frac{3}{2},3)$

$\therefore\cos \theta=\frac{\frac{9}{2}+\frac{9}{2}}{\sqrt{9+9+0}\sqrt{\frac{9}{4}+\frac{9}{4}+9}}$

$=\frac{9}{\sqrt{18}.\sqrt{\frac{27}{2}}}=\frac{1}{\sqrt{3}}$

$\therefore$ Option (a) is incorrect.

Now, equation of the plane containing the  $\triangle OQS $ is

$\begin{bmatrix}x & y& z \\3 & 3 &0\\3/2 &3/2&3\end{bmatrix}\Rightarrow0\Rightarrow\begin{bmatrix}x &y &z \\1 & 1 &0 \\ 1&1&2\end{bmatrix}=0$

$\Rightarrow  x(2-0)-y(2-0)+z(1-1)=0$

$\Rightarrow  2x-2y=0 $ or x-y=0

$\therefore$ Option  (b) is correct.

 Now, length  of the perpendicular from P(3,0,0) to the plane containing $\triangle OQS $  is 

 $\frac{|3-0|}{\sqrt{1+1}}=\frac{3}{\sqrt{2}}$

 $\therefore$ Option (c)  is correct.

Here, equation of RS is 

 $\frac{x-0}{3/2}=\frac{y-3}{-3/2}=\frac{z-0}{3}=\lambda$

 $\Rightarrow x=\frac{3}{2}\lambda, y=-\frac{3}{2}\lambda+3, z=3\lambda$

 To find the distance from O(0,0) to RS. 

 Let M be the foot of perpendicular.

   $\therefore$       $\overline{OM}\perp\overline{RS}\Rightarrow\overline{OM}.\overline{RS}=0$

  $\Rightarrow  \frac{9\lambda}{4}-\frac{3}{2}\left(3-\frac{3\lambda}{2}\right)+3(3\lambda)=0$

$\Rightarrow  $   $\lambda=\frac{1}{3}$

$\therefore$             $M\left(\frac{1}{2},\frac{5}{2},1\right)$

$\Rightarrow  OM=\sqrt{\frac{1}{4}+\frac{25}{4}+1}=\sqrt{\frac{30}{4}}=\sqrt{\frac{15}{2}}$

$\therefore$   Option (d) is correct

A solution curve of the differential  equation $(x^{2}+xy+4x+2y+4)\frac{\text{d}y}{\text{d}x}-y^{2}=0$ , x>0, passes through the point (1,3) Then , the solution curve

Answer:

Explanation:

Given, $(x^{2}+xy+4x+2y+4)\frac{\text{d}y}{\text{d}x}-y^{2}=0$

$\Rightarrow$    $[(x^{2}+4x+4)+y(x+2)]\frac{dy}{dx}-y^{2}=0$

$\Rightarrow$    $[(x+2)^{2}+y(x+2)]\frac{dy}{dx}-y^{2}=0$

Put x+2=X  and y=Y, then

$(X^{2}+XY)\frac{dY}{dX}-Y^{2}=0$

$\Rightarrow$     $X^{2}dY+XYdY-Y^{2}dX=0$

$\Rightarrow$    $X^{2}dY+Y(XdY-YdX)=0$

$\Rightarrow$    $-\frac{dY}{Y}=\frac{XdY-YdX}{X^{2}}$

$\Rightarrow$   $-d(\log|Y|)=d(\frac{Y}{X})$

On integrating both sides , we get,

 $-\log|Y|=\frac{Y}{X}+C$

where x+2=X and  y=Y

$\Rightarrow$      $-\log|y|=\frac{Y}{x+2}+C$              ...........(i)

 Since, it passes through the point (1,3)

$\therefore$        $-\log 3 =1+C$

$\Rightarrow$  $C =-1-\log 3$

$=-(\log e +\log 3)$

 $=-\log 3e $

$\therefore$  Eq. (i) becomes

 $\log |y|+\frac{y}{x+2} -\log (3e)=0$

 $\Rightarrow$       $\log\left( \frac{|y|}{3e}\right)+\frac{y}{x+2}=0$       ........(ii)

Now, to check option (a)   y=x+2 intersects the curve.

 $\Rightarrow$     $\log (\frac{|x+2|}{3e})+\frac{x+2}{x+2}=0$

 $\Rightarrow$    $\log (\frac{|x+2|}{3e})=-1$

 $\frac{|x+2|}{3e}=e^{-1}=\frac{1}{e}$  

 $\Rightarrow$   ${|x+2|}=3 $  or  $x+2=\pm3$

 $\therefore$    x=1, -5 (rejected) , as x>0   [given]

 $\therefore$   x=1 only one solution

 Thus ,(a)  is the correct  answer.

To check option (c) we have

 $y=(x+2)^{2}$

and    $\log(\frac{|y|}{3e})+\frac{y}{x+2}=0$

$\Rightarrow$  $\log\left[\frac{|x+2|^{2}}{3e}\right]+\frac{\left(x+2\right)^{2}}{x+2}=0$

$\Rightarrow$   $\log\left[\frac{|x+2|^{2}}{3e}\right]=-\left(x+2\right)$

$\Rightarrow$     $\frac{(x+2)^{2}}{3e}=e^{-(x+2)}$

or     $(x+2)^{2}.e^{x+2}=3e$

$\Rightarrow$   $e^{x+2}=\frac{3e}{(x+2)^{2}}$

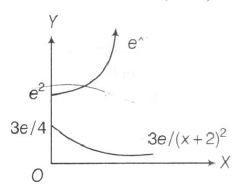
Clearly, they have no solution.

 To check option (d),

$y=(x+3)^{2}$

i.e,      $\log \left[ \frac{|x+3|^{2}}{3e}\right]+\frac{(x+3)^{2}}{(x+2)}=0$

 To check the number of solutions,

  Let  $g(x)= 2\log (x+3)+\frac{(x+3)^{2}}{(x+2)}-\log (3e)$

$\therefore$      $g'(x)=\frac{2}{x+3}+$

$\left( \frac{(x+2).2(x+3)-(x+3)^{2}.1}{(x+2)^{2}}\right)-0$

 $=\frac{2}{x+3}+\frac{(x+3)(x+1)}{(x+2)^{2}}$

Clearly, when x>0, then  ,g' (x)>0

$\therefore$    g(x) is increasing , when x>0

Thus ,when x.0, then g(x) >g(0)

$g(x)>\log (\frac{3}{e})+\frac{9}{4}>0$

Hence, there is no solution

Thus, option  (d) is true

A computer producing factory has only two plants   $T_{1}$   and $T_{2}$. Plant  $T_{1}$ produces 20% and $T_{2}$ produces 80% of the total computers produced.7% of computers produced in the factory turn out to be defective. It is known that P(computer turns out to be defective. given that it is produced in plant $T_{1}$)= 10P  (Computer turns out to be defective, given that it is produced in plant $T_{2}$, where P(E) denotes the probability of an event E. A computer produced in the factory is randomly selected and it does not turn out to be defective. Then, the probability  that it is  produced  in plant $T_{2}$, is

Answer:

Explanation:

Let x=P   (computer turns out to be defective, given that it is produced in plant $T_{2}$)

$\Rightarrow$        $x=P(\frac{D}{T_{2}})$           .............(i)

where  , D= Defective computer

$\therefore$ P (computer  turns out to be defective given that is produced  in plant  $T_{1}$)=10x

 i.e,     $P(\frac{D}{T_{1}})=10x$            .......(ii)

Also,   $P(T_{1})=\frac{20}{100}$  and  $P(T_{2})=\frac{80}{100}$

Given, P  (defective computer )=  $\frac{7}{100}$

Using law of total probability,

 $P(D)=9(T_{1}).P(\frac{D}{T_{1}})+ P(T_{2}).P(\frac{D}{T_{2}})$

$\therefore$       $\frac{7}{100}=(\frac{20}{100}).10x+(\frac{80}{100}).x$

$\Rightarrow$     7= (280)x

$\Rightarrow$     $x=\frac{1}{40}$          ..........(iii)

$\therefore$    $P(\frac{D}{T_{2}})=\frac{1}{40}$  and   $P(\frac{D}{T_{1}})=\frac{10}{40}$

$\Rightarrow$    $P(\frac{\overline{D}}{T_{2}})=1-\frac{1}{40}=\frac{39}{40}$

and    $P(\frac{\overline{D}}{T_{1}})=1-\frac{10}{40}=\frac{30}{40}$                       .........(iv)

 Using Baye's theorem,

 $P(\frac{T_{2}}{D})=\frac{P(T_{2}\cap\overline{D})}{P(T_{1}\cap\overline{D})+P(T_{2}\cap\overline{D})}$

 $=\frac{P(T_{2}).P(\frac{\overline{D}}{T_{2}})}{P(T_{1}).P(\frac{\overline{D}}{T_{1}})+P(T_{2}).P(\frac{\overline{D}}{T_{2}})}$

 $=\frac{\frac{80}{100}.\frac{39}{40}}{\frac{20}{100}.\frac{30}{40}+\frac{80}{100}.\frac{39}{40}}=\frac{78}{93}$

Let   $S= [ x\epsilon (-\pi,\pi):x\neq0, \pm\frac{\pi}{2}],$ The sum of all distinct solutions of the equation $\sqrt{3}\sec x+ cosec x+2(\tan x-\cot x)=0$  in the set S is equal to 

Answer:

Explanation:

Given,    $\sqrt{3} \sec x+ cosec x+2(\tan x-\cot x)=0,$

$(-\pi <x<\pi)-(0,\pm \pi/2)$

$\Rightarrow$     $\sqrt{3}\sin x+\cos x+2 (\sin^{2}x-\cos^{2}x)=0$

$\Rightarrow$     $ \sqrt{3}\sin x +\cos x-2\cos2x=0$

  Multiplying and dividing by   $\sqrt{a^{2}+b^{2}}.$ i.e

 $\sqrt{3+1}=2$  , we get

 $2(\frac{\sqrt{3}}{2}\sin x+\frac{1}{2}\cos x)-2\cos2x=0$

=  $(\cos x.\cos\frac{\pi}{3}+\sin x.\sin\frac{\pi}{3})-\cos 2x=0$

  $\cos (x-\frac{\pi}{3})=\cos 2x$

$\therefore$       $\therefore2x=2n\pi\pm (x-\frac{\pi}{3})$

  [since., $\cos\theta=\cos \alpha \Rightarrow\theta=2n\pi\pm \alpha]$

 $\Rightarrow$     $2x=2n\pi+x-\frac{\pi}{3}$

 or      $2x=2n\pi-x+\frac{\pi}{3}$   

 $\Rightarrow x=2n\pi-\frac{\pi}{3}or 3x=2n\pi+\frac{\pi}{3}$

  $\Rightarrow x=2n\pi-\frac{\pi}{3}or x=\frac{2n\pi}{3}+\frac{\pi}{9}$

$\therefore$  $   x=-\frac{\pi}{3}$ or    $   x=\frac{\pi}{9}.-\frac{5\pi}{9}.\frac{7\pi}{9}$

Now, sum of all distinct solutions

$=-\frac{\pi}{3}+\frac{\pi}{9}-\frac{5\pi}{9}+\frac{7\pi}{9}=0$

• Advanced 2016 - Physics 2016
• Advanced 2016 - Chemistry 2016
• Advanced 2016 - Mathematics 2016